
When I walked into Pierre Pica's cramped Paris apartment, I was overwhelmed by the stench of mosquito repellent. Pica, a linguist, had just returned from spending five months with a community of Indians in the Amazon rainforest, and he was disinfecting the gifts he had brought back. I asked how the trip had been. "Difficult," he replied.
Alex's Adventures in Numberland
by Alex Bellos
448pp,
Bloomsbury Publishing PLC,
£17.99
For the last 10 years, the focus of Pica's work has been the Munduruku: an indigenous group of about 7,000 people in the Brazilian Amazon whose language has no tenses, no plurals and no words for numbers beyond five. To get to the Munduruku, Pica had to wait for some locals to take him to their territory by canoe.
"How long did you wait?" I inquired.
"I waited quite a lot. But don't ask me how many days."
"So, was it a couple of days?" I suggested tentatively. A few seconds passed as he furrowed his brow: "It was about two weeks."
The more I pushed Pica for facts and figures, the more reluctant he was to provide them. "When I come back from Amazonia, I lose sense of time and sense of number, and perhaps sense of space." This inability to give me quantitative data was part of his culture shock. He had spent so long with people who can barely count that he had lost the ability to describe the world in terms of numbers.
No one knows for certain, but numbers are probably no more than about 10,000 years old. By this, I mean a working system of words and symbols for numbers. One theory is that such a practice emerged together with agriculture and trade, as numbers were an indispensable tool for taking stock and making sure you were not ripped off.
Numbers are so prevalent in our lives that it is hard to imagine how people survive without them. Yet while Pica stayed with the Munduruku, he easily slipped into a numberless existence. He slept in a hammock. He went hunting and ate tapir, armadillo and wild boar. He told the time from the position of the sun. If it rained, he stayed in; if it was sunny, he went out. There was never any need to count.
Still, I thought it odd that numbers larger than five did not crop up at all in Amazonian daily life. What if you ask a Munduruku with six children how many kids they have? "He will say, 'I don't know,'" Pica said. "It is impossible to express."
Anyway, he added, the issue was a cultural one. It was not the case that the Munduruku counted his first child, his second, third, fourth and fifth, and then scratched his head because he could go no further. For the Munduruku, the whole idea of counting children is ludicrous. Why would a Munduruku adult want to count his children? They are looked after by all the adults in the community, Pika said, and no one is counting who belongs to whom.
The reason for researching the mathematical abilities of these people who count only on one hand is to discover the nature of our basic numerical intuitions. In one of his most fascinating experiments, Pica examined the Indians' spatial understanding of numbers. How did they visualise numbers when spread out on a line? In the modern world we do this all the time – on tape measures, rulers, graphs and houses along a street.
Pica tested them using sets of dots on a screen. Each volunteer was presented with a figure of an unmarked line. To the left side of the line was one dot; to the right, 10 dots. Each volunteer was then shown random sets of between one and 10 dots. For each set, the subject had to point at where on the line he or she thought the number of dots should be located. Pica moved the cursor to this point and clicked. Through repeated clicks, he could see exactly how the Munduruku spaced numbers between one and 10.
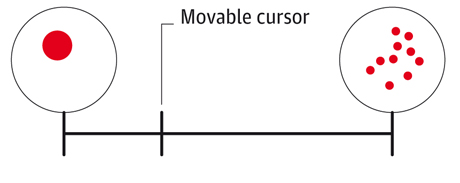
When American adults were given this test, they placed the numbers at equal intervals along the line. The Munduruku, however, responded quite differently. They thought that intervals between the numbers started large and became progressively smaller as the numbers increased. It is generally considered a self-evident truth that numbers are evenly spaced. It is the basis of all measurement and science. Yet the Munduruku visualise magnitudes in a completely different way.
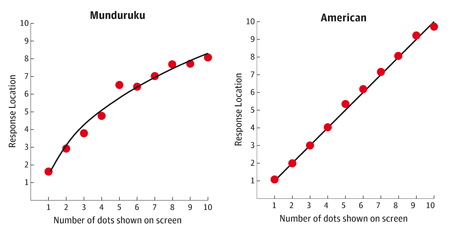
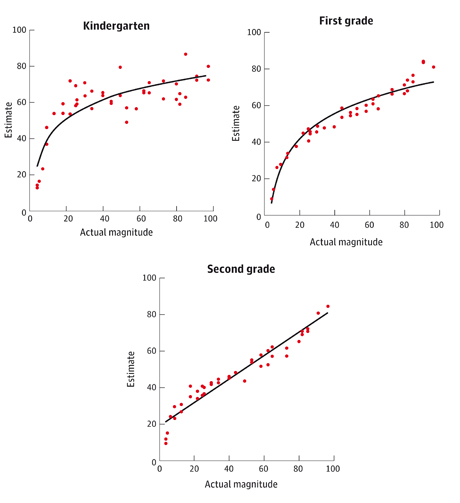
When numbers are spread out evenly on a ruler, the scale is called linear. When numbers get closer as they get larger, the scale is called logarithmic. And it turns out the logarithmic approach is not exclusive to Amazonian Indians – we are all born conceiving numbers this way. In 2004, Robert Siegler and Julie Booth at Carnegie Mellon University in Pennsylvania presented a similar version of the number-line experiment to a group of kindergarten pupils (average age: 5.8 years), first-graders (6.9) and second-graders (7.8). The results showed in slow motion how familiarity with counting moulds our intuitions. The kindergarten pupil, with no formal maths education, maps out numbers logarithmically. By the first year at school, when the pupils are being introduced to number words and symbols, the curve is straightening. And by the second year at school, the numbers are at last evenly laid out along the line. There is a simple explanation. Imagine a Munduruku is presented with five dots. He will study it closely and see that five dots are five times bigger than one dot, but 10 dots are only twice as big as five dots. The Munduruku – and the children – seem to be making their decisions about where numbers lie based on estimating the ratios between amounts. When considering ratios, it is logical that the distance between five and one is much greater than the distance between 10 and five. And, if you judge amounts using ratios, you will always produce a logarithmic scale.
It is Pica's belief that understanding quantities in terms of estimating ratios is a universal human intuition, due to the fact that ratios are much more important for survival in the wild. Historically, faced with a group of adversaries, we needed to know instantly whether there were more of them than us. When we saw two trees, we needed to know instantly which had more fruit hanging from it. In neither case was it necessary to enumerate every enemy or every fruit individually. The crucial thing was to be able to make quick estimates of the relevant amounts and compare them; in other words to make approximations and judge their ratios.
The logarithmic scale also takes account of perspective. For example, if we see a tree 100 metres away and another 100 metres behind it, the second 100 metres looks shorter. To a Munduruku, the idea that every 100 metres represents an equal distance is a distortion of how he perceives the environment. Exact numbers provide us with a linear framework that contradicts our logarithmic intuition.
We live with both a linear and a logarithmic understanding of quantity. For example, our understanding of the passing of time tends to be logarithmic. We often feel that time passes faster the older we get. Yet it works in the other direction too: yesterday seems a lot longer than the whole of last week.
Our deep-seated logarithmic instinct surfaces most clearly when it comes to thinking about very large numbers. For example, we can all understand the difference between one and 10. It is unlikely we would confuse one pint of beer and 10 pints of beer. Yet what about the difference between a billion gallons of water and 10 billion gallons of water? Even though the difference is enormous, we tend to see both quantities as quite similar – very large amounts of water. Likewise, the terms millionaire and billionaire are thrown around almost as synonyms – as if there is not so much difference between being very rich and very, very rich.
Stanislas Dehaene is perhaps the leading figure in the cross-disciplinary field of numerical cognition. He started off as a mathematician, and is now a neuroscientist, a professor at the Collège de France and one of the directors of NeuroSpin, a state-of-the-art research institute near Paris. In 1997, he was having lunch in the canteen of Paris's Science Museum with the Harvard development psychologist, Elizabeth Spelke. They had sat down, by chance, next to Pierre Pica. Pica brought up his experiences with the Munduruku and, after excited discussions, the three decided to collaborate. The chance to study a community that doesn't have counting was a wonderful opportunity for new research.
Dehaene devised experiments for Pica to take to the Amazon, one of which was very simple: he wanted to know just what they understood by their number words. Back in the rainforest, Pica assembled a group of volunteers and showed them varying numbers of dots on a screen, asking them to say aloud the number of dots they saw. The Munduruku numbers are:
1 pug
2 xep xep
3 ebapug
4 ebadipdip
5 pug pogbi
When there was one dot on the screen, the Munduruku said "pug". When there were two, they said "xep xep". But beyond two, they were not precise. When three dots showed up, "ebapug" was said only about 80% of the time. The reaction to four dots was "ebadipdip" in only 70% of cases. When shown five dots, "pug pogbi" was managed only 28% per cent of the time, with "ebadipdip" given instead in 15% of answers. In other words, for three and above the Munduruku's number words were really just estimates. They were counting "one", "two", "three-ish", "four-ish", "five-ish". Pica started to wonder whether "pug pogbi", which literally means "handful", even really qualified as a number. Maybe they could not count up to five, but only to four-ish?
Pica also noticed an interesting linguistic feature of their number words. From one to four, the number of syllables of each word is equal to the number itself. This observation really excited him. "It is as if the syllables are an aural way of counting," he said. In the same way that the Romans counted I, II, III and IIII but switched to V at five, the Munduruku started with one syllable for one, added another for two, another for three, another for four – but did not use five syllables for five. When the number of syllables was no longer important, the word was maybe not a number word at all. "This is amazing, since it seems to corroborate the idea that humans possess a number system that can only track up to four exact objects at a time," Pica said.
He also tested the Munduruku's abilities to estimate large numbers. In one test, the subjects were shown a computer animation of two sets of several dots falling into a can. They were then asked to say if these two sets added together in the can – no longer visible for comparison – amounted to more than a third set of dots that then appeared on the screen.
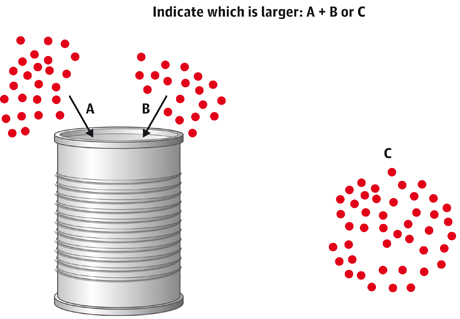
This tested whether they could calculate additions in an approximate way. They could, performing just as well as a group of French adults given the same task. In a related experiment, Pica's computer screen showed an animation of six dots falling into a can and then four dots falling out. The Munduruku were asked to point at one of three choices for how many dots were left in the can. In other words, what is six minus four? This test was designed to see if the Munduruku understood exact numbers for which they had no words.
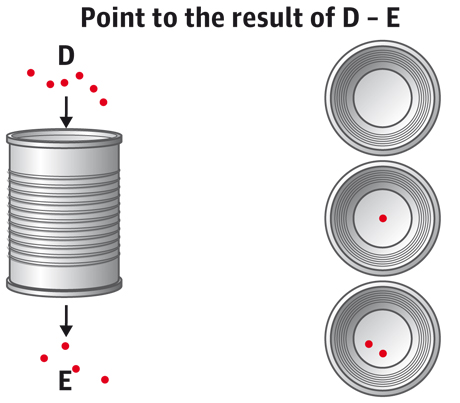
They could not do the task. When shown the animation of a subtraction that contained either six, seven or eight dots, the solution always eluded them. "They could not calculate even in simple cases," said Pica.
The results of these dot experiments showed that the Munduruku were very proficient in dealing with rough amounts, but were abysmal in exact numbers above five. Pica was fascinated by the similarities this revealed between the Munduruku and westerners: both had a fully functioning, exact system for tracking small numbers and an approximate system for large numbers. The significant difference was that the Munduruku had failed to combine these two independent systems together to reach numbers beyond five. Pica said this must be because, for them, keeping the systems separate was more useful. And the fact that some Munduruku had learned to count in Portuguese but still failed to grasp basic arithmetic, was an indication of just how powerful their own mathematical system was and how well suited it was to their needs.
Could it be that humans need words for numbers above four in order to have an exact understanding of them? Professor Brian Butterworth, of University College London, believes that we don't. He thinks that the brain contains a ready-built capacity to understand exact numbers, which he calls the "exact number module".
According to his interpretation, humans understand the exact number of items in small collections, and by adding to these collections one by one we can learn to understand how bigger numbers behave. He has been conducting research in the only place outside the Amazon where there are indigenous groups with almost no number words: the Australian outback.
The Warlpiri Aboriginal community lives near Alice Springs and has words only for one, two and many. The Anindilyakwa of Groote Eylande in the Gulf of Carpentaria have words only for one, two, three (which sometimes means four) and many.
In one experiment with children of both groups, a block of wood was tapped with a stick up to seven times and counters were placed on a mat. Sometimes the number of taps matched the number of counters, sometimes not. The children were perfectly able to say when the numbers matched and when they didn't. Butterworth argued that to get the answer right, the children were producing a mental representation of exact number that was abstract enough to represent both auditory and visual enumeration. These children had no words for the numbers four, five, six and seven, yet were perfectly able to hold those amounts in their heads. Words were useful to understand exactness, Butterworth concluded, but not necessary.
Another important focus of Butterworth's work – and of Dehaene's – is a condition called dyscalculia, or "number blindness". It occurs in an estimated 3-6% of the population. Dyscalculics do not "get" numbers the way most people do.
For example, which of these two figures is biggest? 65 or 24? Almost all of us will get the correct answer in less than half a second. If you have dyscalculia, however, it can take up to three seconds. The nature of the condition varies from person to person, but those diagnosed with it often have problems in correlating the symbol for a number, say 5, with the number of objects the symbol represents. They also find it hard to count. Sufferers tend to rely on alternative strategies to cope with numbers in everyday life; for instance by using their fingers more. Severe dyscalculics can barely read the time.
Understanding dyscalculia has a social urgency, since adults with low numeracy are much more likely to be unemployed or depressed than their peers. Much of the research is behavioural, such as the screening of tens of thousands of schoolchildren in which they must say which of two numbers is the biggest. Some is neurological, in which magnetic resonance scans of dyscalculic and non-dyscalculic brains are studied to see how their circuitry differs. Gradually, a clearer picture is emerging of what dyscalculia is – and of how the number sense works in the brain.
Neuroscience, in fact, is providing some of the most exciting new discoveries in the field of numerical cognition. It is now possible to see what happens to individual neurons in a monkey's brain when that monkey thinks of a precise number of dots.
Andreas Nieder, at the University of Tübingen in southern Germany, trained rhesus macaques to think of a number. He did this by showing them one set of dots on a computer, then, after a one-second interval, showing another set of dots. The monkeys were taught that if the second set was equal to the first set, pressing a lever would earn them a reward of a sip of apple juice. If the second set was not equal to the first, then there was no apple juice.
After about a year, the monkeys learned to press the lever only when the number of dots on the first and second screens was equal. Nieder and his colleagues reasoned that during the one-second interval between screens, the monkeys were thinking about the number of dots they had just seen.
Nieder decided he wanted to see what was happening in the monkeys' brains when they were holding the number in their heads. So, he inserted an electrode two microns in diameter through a hole in their skulls and into the neural tissue. (At that size, an electrode is tiny enough, apparently, to slide through the brain without causing damage or pain.)
When the monkeys thought of numbers, Nieder saw that certain neurons became very active. On closer analysis, he made a fascinating discovery: the number-sensitive neurons reacted with varying charges depending on the number that the monkey was thinking of at the time. Furthermore, when a monkey was thinking "four", the neurons that preferred four were the most active, of course – but the neurons that preferred three and the neurons that preferred five were also active, though less so, because its brain was also thinking of the numbers surrounding four. "It is a noisy sense of number," explained Nieder. "The monkeys can only represent cardinalities in an approximate way."
It is almost certain that the same thing happens in human brains. Which raises an interesting question: if our brains can represent numbers only approximately, then how were we able to "invent" numbers in the first place?
"The 'exact number sense' is a [uniquely] human property that probably stems from our ability to represent number very precisely with symbols," concluded Nieder. Which reinforces the point that numbers are a cultural artefact, a man-made construct, rather than something we acquire innately.

3 comments:
This was a very interesting read!
I am a severe dyscalculic myself- I can read the time, but it's just numbers- for example I can look at the clock on my computer RIGHT NOW, and it says 11:34. That doesn't mean anything to me. I have no concept of time. I can't tell the difference between half an hour and five hours; and even if I try to look at a calender often, I may lose track of time so badly as to drastically mistake the month.
That's just one of the many ways dyscalculia can affect thought processes. (I also have a very poor sense of distance.)
I'm not sure I like hearing it referred to as "number blindness", though, because it can affect so much more than mathematic and numerical ability.
Of course, that then brings into question what concepts are "human constructs", and how the way numbers are thought of also affects those concepts.
Just some thoughts. You gave me an interesting read at least.
Hi Jason. Many thanks for your comments, indeed. I can see that it´s a very important topic to you and I have to say you are the first person that I heard about dyscalculia from. I took this article from the UK´s The Guardian newspaper - they published it in the daily supplement called G2 and it was indeed very long for today´s standard average article in a mass circulation paper. I am terrible with numbers myself, I used to be totally blocked in Maths hour when at Primary and Secondary but I don´t think I have anything close to what you describe about yourself. I wonder how you cope in every day life with this condition - I mean, it´s a big handicap or is it just ok? Just questions that come to my mind, you don´t have to answer them, of course. And thanks again for sharing your thoughts here as I am not used to see any comments at all in my blog! Except my very good friend Chris, no-one writes here anything. Well, knowing that the total audience is about 6 people, one contributor is not a bad number! :-)
Feel free to ask any questions you like, I don't mind.
How I cope... Well, with the actual mathematics side of things, it's difficult. I'm incredibly intelligent, so I managed to learn patterns and methods to allow me to be able to work with numbers. It's not easy- in fact, learning mathematics is the ONLY thing I've ever really had trouble with. (Excepting, of course, other things which involve maths.) The difficulty is that I'm so used to being able to learn things with ease- even now, as an adult, I'm trying to "train my brain" to be able to handle maths easier, and it's a constant struggle- but my pride suffers more than anything else!
There are other things which are harder, though- I don't find my mathematical ability is too much of an issue, because there's not much call for it any more. After all, I can always use a calculator when I need to.
The time issue can be a problem- I wear a watch whenever I need to keep an eye on the time, and have developed a habit of alloting times for things. For example, I might allot myself an hour to get ready in the morning- and any time left over I can spend doing my own thing. I have no idea how long it actually takes- much less than an hour, I'm sure- but this way I ensure I give myself enough time.
However, even when I get up at- for example- 5:30AM, I can find I've run out of time and have no idea how or why. I just can't wrap my head around the concept of time, and it's confusing.
Distance is similar- travelling to new places whilst on a timer can be stressful, especially if I'm trying to follow directions. That's not too big an issue, though.
Anyway. To properly answer your question- it's not a BIG handicap, and I've learned ways around it. It definately has an impact on my day-to-day life, but it's not a big deal. And if I were given the choice between losing both my high intelligence levels and my dyscalculia, or staying as I am- well, there's really no question about it, in all honesty.
Aaand that was very rambly.
Post a Comment